Electrochemistry Encyclopedia -- Magnetic effects

Return to: Encyclopedia Home Page – Table of Contents – Author Index – Subject Index – Search – Dictionary – ESTIR Home Page – ECS Home Page

MAGNETIC EFFECTS IN ELECTROCHEMISTRY

Thomas Z. Fahidy
Department of Chemical Engineering
University of Waterloo
Waterloo, ON N2L 3G1, Canada
(May, 2001, Last revision: April, 2008)

Suppose that you are asked to name an object as common as a toothbrush. Being a technical person, your answer is: an electric motor. Your answer is. excellent! There would be no modern life without electric motors, which operate on a very simple principle: the interaction of electric and magnetic fields, resulting in rotating motion.

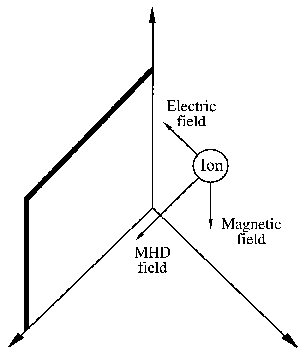Fig. 1. Ionic movement is generated in a medium by the coupling of an electric and a magnetic field. The direction of movement is perpendicular to the fields. The resulting "sweep" action along the solid surface generates strong local turbulence enchancing mass transport at the interface (see Appendix).

The same principle applies when ions and electrons are exposed in a liquid medium to combined electric and magnetic fields. Motion is generated, as shown in Figure 1, whose velocity is perpendicular to the direction of the generating fields. In a liquid solution with an astronomical number of ions "swimming" in a big pool of solvent (for example water), the outcome of the field interaction might appear to be chaotic and dissipated in randomness. Fortunately, this is not what happens.

Glancing again at Figure 1, imagine ions, forced by the magnetic and electric fields, sweeping by the solid plate. The sweeping motion generates considerable turbulence in the tiny liquid layer adjacent to the plate, called the interface. This interfacial turbulence is at the bottom of most, but not all, magnetic phenomena in electrolysis, that is when electric current flows through an electrolyte solution in a cell held between the pole faces of a magnet. An important practical result, magnetically enhanced cathodic deposition of metals (in electroplating or electrowinning), created the science and engineering of magnetoelectrolysis.

All in all, magnets exert a strong influence on electrode processes. They can modify deposit structure, increase the rate of deposition of the reaction product(s), change flow patterns, and increase the intensity of mixing. Magnetoelectrochemistry is a fast growing new field of scientific and technical endeavor.

Early observations

Ironically, research in this field was started in a different direction by the distinguished scientist Michael Faraday (1791-1867) who could perhaps be called the Mozart of electromagnetism, on account of his talent and virtuosity. Early studies probed primarily magnetic influence on electrolyte properties (for example electric conductivity, viscosity, and diffusivity), and the magnitude of a very small induced potential field, called the Hall effect. With continuing improvement of their precision over several decades, the Hall effect in electrolytes was finally identified via impressive experimental techniques. The effect is many orders of magnitude smaller than in solid conductors and gaseous plasmas, but the smallness of its magnitude is well compensated by the impetus it gave to the development of theoretical foundations of magnetoelectrochemical science. Similarly small, but highly reproducible local temperature variations (amounting to fractions of a degree) have been also demonstrated to exist in various electrolytes exposed to combined magnetic and electric fields by scientists at the University of Rheims, France (notably by Emmanuel Tronel-Peyroz and Alain Olivier). Not surprisingly, interest in these phenomena was at one time professed only by a small number of dedicated investigators. Magnetoelectrochemistry seemed to be confined to the realm of esoteric curiosity, exciting a few and leaving many indifferent. One scientist stated flatly in his book (written in the forties) on electrochemistry that the Hall effect did not exist at all in aqueous electrolytes! This young and fledgling science needed a strong push for survival.

Coming of age

The required strong push came from the alliance of magnetohydrodynamics (MHD) and convective diffusion theory (CDT). MHD on its own offered a promising path to power generation, high precision pumping and flow metering, but electrochemistry was not included in its domain. CDT, on the other hand, established the importance of mass transport and fluid mechanics for modern electrochemistry. Combination of the two fields empowered researchers to design appropriate experimental scenarios to study magnetically induced phenomena on a scale much higher than previously. Cathodic deposition of metals, flow propagation, and more recently oriented crystal growth are major avenues of demonstrating tangible magnitudes of the magnetic field effect. Magnetoelectrochemistry has arrived at its mature stage.

Magnetoelectrolysis

Table I. Copper deposition in a magnetoelectrolytic cell
Magnetic flux density (mT)	Limiting current density (A/m²)
4	355
110	359
200	369
285	374
460	380
785	389
Notes: The fundamental unit of the magnetic flux density is the tesla (T), its one-thousandth is the millitesla (mT). 4 mT is the residual flux density, that is with no excitation of the electromagnet. In the experiment carried out by S. Mohanta in his MASc thesis under the author's supervision, deposition took place at 25^oC (77^oF) from an aqueous 0.534 molar cupric sulfate – 1.59 molar sulfuric acid solution and active electrode area of 53.22 cm²; the parallel copper electrode plates were 4.61 cm apart. The electrodes were vertical and the magnetic and electric fields mutually perpendicular.

Pure metals may conveniently be deposited from electrolyte solutions or molten electrolytes (in electroplating or electrowinning). The process is especially inviting for precious metals (for example gold and silver) and copper, nickel, zinc, etc., although simultaneous hydrogen evolution in a number of cases may thwart deposit quality. The rate of deposition per unit substrate area, measured as current density, is controlled by the electrode potential. The higher the potential, the higher the current density up to a certain point, beyond which the current cannot increase even if the potential is increased over a wide range. This is the limiting current density for a given depositing species, and its magnitude depends on electrolyte properties and design features of the electrolytic cell. If electrolysis is carried out between the pole faces of a magnet, the limiting current density for a species increases in proportion to the strength of the magnetic field, upon proper matching of the magnetic and the electric fields. The strength of the magnetic field may be expressed in terms of the magnetic flux density. A typical set of experimental observations during the magnetoelectrolytic deposition of copper indicates an essentially linear dependence of the maximum deposition rate on the magnetic flux density, but limiting current densities have been shown in the literature to vary with the power (exponent) of the magnetic flux density ranging from 0.25 to 1.64, depending on cell design, electrolyte composition and the metal species. See Table I.

Apart from increased deposition rates, magnetic fields offer the bonus of providing evenness and excellent adhesion of the metal deposits on their substrates, even at current densities where deposit quality would be poor in their absence.

Preferential flow propagation and mixing

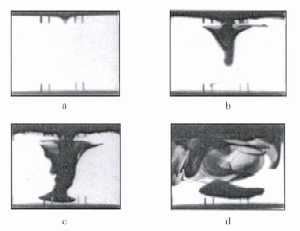Fig. 2. Propagation of convective flow in combined electric and magnetic fields, see text. (M.S. Quraishi and T.Z. Fahidy, A Study of Convective Flow Patterns Via Electrochemical Means, Paper 80-HT-93, Joint ASME/AIChE National Heat Transfer Conference, July 27-30, 1980, Orlando, FL. – With permission of the ASME.)

A particularly interesting and potentially useful property of magnetic fields is the creation of preferential flow patterns or channels in liquid media. This phenomenon can easily be monitored by dyes used in analytical chemistry. The dyes change color due to a minute increase or decrease of hydrogen ions in the solution at a conveniently chosen solid-liquid interface. The propagation of flow generated at the interface into the bulk solution is tagged by the dye (also called the indicator) whose color is much different (usually much darker) from the color of the dye in the unaffected zones of the liquid. The propagation pattern can easily be seen by the naked eye, and photographed by conventional means. Such observations demonstrate convincingly that MHD flow created by magnetic field imposition on flow cells with an electrified solid surface propagates via specific, preferential channels, and that significant portions of the liquid medium behave as "dead zones" for relatively long times. Flow generated at horizontal conducting surfaces in parallel magnetic/electric fields propagates according to a snowballing sequence, which starts at a small local area on the surface, where the electric current is slightly non-uniform at the onset. Current non-uniformity is an essential feature, because MHD theory predicts no magnetic field effect if the two fields are strictly parallel and uniform. A solid surface, however, is never absolutely uniform, and even microscopic-scale protuberances on the surface are capable of generating non-uniform currents. The interaction of these currents with magnetic fields gives rise to non-uniform flow, which becomes increasingly pronounced in time. This mode of flow propagation, which fluid mechanics experts call "anisotropic", may be useful to accelerate fluid transport in certain conduits.

An example of this phenomenon is shown in Figure 2, showing the propagation of convective flow in combined electric and magnetic fields. At the onset of the experiment (zero time) the transparent analytical indicator changes its colour to dark blue due to a local shortage of hydrogen ions at the upper electrified horizontal surface. Microscopic surface nonuniformity creates a small conical-shaped flow pattern about twenty seconds later (a) Propagation remains confined to the central zone of the cell, keeping its conical shape, which simultaneously expands downwards and horizontally, while rotating around the vertical axis (b, about two minutes later). While rotation continues, the funnel keeps expanding and begins to lose its conical shape (c, five minutes later). At large times (d, ten minutes later) the flow tends to be chaotic, but the light-coloured areas indicate the survival of dead zones. If the magnetic field were absent, a sluggish and uniform downward movement of the tagged flow would indicate isotropic convection.

Magnetic field gradients generate wavy surfaces

Fig. 3. Surface waves are generated by the interaction of an electric field with a nonuniform (gradient) magnetic field.

Suppose you arrange an electrolytic cell such that when you drew a line in your mind connecting the edges of the magnetic pole faces, this imaginary line crosses the center of the cell. You will generate in this simple manner a magnetic field gradient because at every point in the cell the magnitude of the magnetic flux density would be different. This gradient and the electric field will create a strong turbulent motion in the liquid. If the gradient is large enough, the liquid surface will become wavy, and the liquid may even spill out of the cell. Rapid mixing in instances where mechanical agitation is impossible or undesirable is one practical application envisaged for this phenomenon. An example is shown in Figure 3. In this experimental cell a mixture of aqueous cupric sulfate and sulfuric acid was contained between two concentric cylindrical copper electrodes ("inner" cell) and between the outer cylindrical glass wall and one of the electrodes ("outer" cell). If the force generated by the interacting fields is large, the electrolyte surface in the inner cell, located in the nonuniform magnetic field, will undulate. The force may be made so strong that high amplitude waves will appear, and portions of the inner cell electrolyte will spill into the outer cell. In the doctoral project of S. Mohanta (under the author's supervision) force magnitudes generated in initial "path-finding" experiments were sufficiently large to cause spilling from the outer cell onto the laboratory floor.

Do you need a compact deposit? Think magnet!

Fig. 4. The 2D growth of silver shows the densification effect of a magnetic field imposed vertically with respect to the horizontal growth plane: (left) in the absence of a magnetic; (center) magnetic flux density at 4 tesla, and (right) at 8 tesla. In each case the process time was 150 minutes.

Metal layers deposited from appropriate electrolytes in magnetic fields have attractive qualities of adhesion, smoothness, reflectiveness ("shininess"), but we do not know exactly, why. A typical example (see Figure 4) is the growth pattern of silver metal leaves in electroless deposition between two glass plates, where growth is two-dimensional, in experiments conducted by I. Mogi, Institute for Materials Research, Tohoku University, Japan. Without a magnetic field the growth is an uneven sprawl of fractal-like branches. If a magnetic field is imposed, the branches become increasingly regular and densely spaced as the strength of the field is increased. Eventually, an almost circular deposit is obtained. Similar observations have been made in the case of some other metals and polymers; the growth pattern is a fingerprint of substance, as well as the magnitude and direction of the magnetic flux density. With an eventually thorough understanding of these interactions, we will be able to "tailor-make" deposit structures with a desired degree of compactness, fractal dimensions, and shape.

Where are we in 2008?

It commonly happens in science and engineering that we have (at least tentative) theories to explain experimental phenomena, but only a modest amount of experimental data. In magnetoelectrochemistry the situation is reversed. No cogent or comprehensive theory exists at this time to explain the fast-growing body of observations under one big umbrella, although MHD, the theory of paramagnetism, the theory of convective diffusion, and certain other theories have been called upon to provide at least an approximate understanding of the experimental paradigm. There is a need for an all-encompassing theoretical framework, and it is hoped that it will catch up sooner or later with the laboratory, all the more so as experimental investigations continue to reach into new directions.

Recognizing the need for some focusing of efforts, the May 20-23 workshop on �Magnetism and Electrochemistry� held in Galway, Ireland in 2001 listed a number of unsolved problems due primarily to (at least currently) limited understanding. Magnetic field effects on morphology; the origin of magnetic anisotropy; anomalous codeposition phenomena; homogeneity of electrodeposited alloys in small trenches (cavities); were earmarked as major items. Three-dimensional mass transfer of magneto-electrochemical origin, turbulence and mass transport in the boundary layer continue to set challenges for the serious experimenter and analyst.

Magnetoelectrolysis has also been proved to provide an excellent means of producing thin metal nanostructured films (for example, hexagonal phase cobalt with a strong preferred <100> orientation, where the magnetic field of flux densities, up to 15 tesla, is antiparallel to the motion of ions). There is a generally strong interest in microscopic and rotational phenomena, local convection, and magneto-convection. Quantification of magnetic force microscopy images, electromagnetic microstructuring, applying magnetic micro-fluid �chips� to reacting media, and the study of chirality (three-dimensional stereoisomerism exhibited by molecules that cannot be superimposed on their mirror image) are just a few important indicators of the rapidly expanding scope of research.

Can a unified theory of magneto-electrochemistry be expected to emerge eventually?

Not unlike modern physics, saddled with the problem of dovetailing cosmological-scale and subatomic observations into a single framework, the science of magneto-electrochemical phenomena is also faced by the conundrum of scale. On a very small scale, for instance, paramagnetism of ions moving in a combined electric-magnetic field plays an important, if not predominant, role. Large-scale MHD forces, on the other hand, relegate paramagnetism at best to a secondary position. The final emergence of a unifying theory remains questionable at this time. See however a discussion in the Appendix.

Appendix

Coupling magnetic and electric fields

The easiest interpretation of the effect of coupling magnetic and electric fields is offered by the MHD Ohm's law. The law relates the electric current density vector "J" to the electric field vector "E", the fluid velocity vector "v", and the magnetic flux density vector "B" by the relationship:

[1] J = σ (E + v × B)

where "σ" is the electrical conductivity of the liquid medium. Consider a simple field configuration, where both magnetic and electric fields are unidimensional and mutually perpendicular, for example E = u_yE_y and B = u_zB_z; the solid electrode plate is in the (x, y) plane ("E_y" and "B_z" are magnitudes in the subscripted direction, and "u_x" "u_y" and "u_z" are unit vectors pointing into the three principal Cartesian directions). Then, the following relationships apply:

[2] v × B = u_xv_yB_z - u_yv_xB_z

[3] j_x = σ v_yB_z

[4] j_y = σ (E_y - v_xB_z)

indicating (a) a magnetic field interaction with current density j_y = σ E_y observed in the absence of the magnetic field, and (b) the appearance of current density component "j_x" in the third Cartesian direction. The resulting two-dimensional motion in the (x, y) plane is particularly pronounced in the vicinity of the solid-liquid interface, where important magnitudes of "v_x" and "v_y" may already exist due to other force fields, such as buoyancy inside a natural convective boundary layer. The magnetic field magnifies this effect and generates locally large turbulence. A thorough analysis of this phenomenon requires a much more involved mathematical apparatus than the MHD Ohm's law (see for example, Hydrodynamic Models in Magnetoelectrolysis, T. Z. Fahidy, Electrochimica Acta, Vol.18, pp 607-614, 1973).

Can a unified theory of magneto-electrochemistry be expected to emerge eventually?

The final emergence of a unifying theory remains questionable at this time. We may envisage, nevertheless, that various mathematical and phenomenological approaches could successfully explore new horizons. One such avenue might be offered by bifurcation and catastrophe theory, well established in the study of modern system dynamics. The key feature here is that a very small change in (physical) parameters can lead to entirely different structures. Beltrami (1998, Example 7.1, p 154) demonstrates the simple bifurcation occurring at a = 0 (called a �fold� catastrophe) for the function y(x, a) = x³/3 � ax. When the parameter a is negative, y(x, a) is a monotone increasing, or a monotone decreasing function. When a = 0, we have the simple cubic equation y = x³, still a monotone increasing or a monotone decreasing function. When a is positive, monotonic behavior no longer exists: there are two local extrema at locations x = -a and x = a, whose values: 2a^3/2/3 and -2a^3/2/3 are symmetrical with respect to the origin. Bifurcations caused by very small changes in physical parameters, for example, conductivity and diffusivity of an electrolyte, at certain locations (for example, in the boundary layer) may arguably yield different solutions to the governing dynamic equations. In this manner, specific vortex motions, convective propagation patterns, etc. may be predictable, at least in a semi-quantitative sense. Magneto-electrochemical systems might, in fact, possess a plethora of bifurcations, waiting to be discovered.

Bibliography

Chirality in Magnetoelectrolysis, I. Mogi and K. Watanabe, invited lecture at the 7^th PAMIR International Conference on Fundamental and Applied MHD, Presqu�ile de Giens, France, Sept. 8-12, 2008.
Effect of High Magnetic Field on Electrodeposited Zn-Ni Alloys, A. Levesque, S. Couchane, J. P. Chopart, and J. Douglade, invited lecture at the 7^th PAMIR International Conference on Fundamental and Applied MHD, Presqu�ile de Giens, France, Sept. 8-12, 2008.
Quasi-periodic Microstructuring of Iron Cylinder Surface under its Corrosion under Combined Electric and Magnetic Fields, O. Y. Gorobets and D. O. Derecha, �Materials Science-Poland� Vol. 24, pp 1017-1025, 2006.
Magnetic Field Effects on the Open Circuit Potential of Ferromagnetic Electrodes in Corroding Solutions, A. Dass, J. A. Counsil, X. Gao, and N. Leventis, �Journal of Physical Chemistry� Vol. 109B, pp 11065-11073, 2005.
Application of Magnetic Micro-Fluid Chip to Chemical and Electrochemical Reactions, R. Aogaki, E. Ito, and M. Ogata, invited lecture at the Joint 15^th Riga and 6^th PAMIR International Conference on MHD, Rigas Jarmala, Latvia, June 27-July 1, 2005.
Nanostructured Magnetic Materials by Magnetoelectrolysis, N. Sulitanu, �Optoelectronics and Advanced Materials� Vol.6, pp 637-640, 2004.
Magnetic Field Effects in Electrochemistry, R. Aogaki, �Magnetohydrodynamics� Vol. 37-1/2, pp 143-150, 2001.
Characteristics of Surfaces Produced via Magnetoelectrolytic Deposition, T. Z. Fahidy, "Progress in Surface Science" Vol.68, pp 155-188, 2001.
Proceedings of The Fourth Meeting, Symposium on New Magneto-Science, Nov. 13-15, 2000, Omiya, Japan, Japan Science and Technology Corporation, National Research Laboratory for Magnetic Science, Kawaguchi, Saitama, Japan 2000.
Proceedings of The Fourth International Pamir Conference on Magnetohydrodynamics at Dawn of Third Millenium, Sept. 18-22, 2000, Giens, France, Vol. 1-2, Sections 7-8, pages 321-398; poster session on magnetoelectrolysis, pages 871-902, LEGI, Grenoble, France, Ben Gurion University, Israel, and Institute of Physics, Riga, Latvia 2000.
Proceedings of the Third Meeting, Symposium on New Magneto-Science '99, Nov. 24-26, 1999, Omiya, Japan, Japan Science and Technology Corporation, National Research Laboratory for Magnetic Science, Kawaguchi, Saitama, Japan 1999.
The Effect of Magnetic Fields on Electrochemical Processes, T. Z. Fahidy, in "Modern Aspects of Electrochemistry" No. 32, Ch 5, pp 333-354, B. E. Conway, J. O'M. Bockris, and R. E. White (editors), Kluwer/Plenum, New York 1999.
Magnetoconvection Phenomena: a Mechanism for Influence of Magnetic Fields on Electrochemical Processes. M. Waskaas and Y. I. Kharkats, "Journal of Physical Chemistry" Vol. 103B, pp 4876-4883, 1999.
Magnetic Field Effects on Fractal Electrodeposits, J. M. D. Coey, G. Hinds, and M. E. G. Lyons, "Europhysics Letters" Vol. 47, pp 267-272, 1999.
Magnetoelectrolysis of Copper, G. Hinds, J. M. D. Coey, and M. E. G. Lyons, �Journal of Applied Physics� Vol. 83, pp 6447-6449,1998.
Electrochemistry with Stationary Disk and Ring-Disk Millielectrodes in Magnetic Fields, N. Leventis, M. Chen, X. Gao, M. Canalas, and P. Zhang, "Journal of Physical Chemistry" Vol. 102B, pp 3512-3522, 1998.
Bifurcation and Chaos Theory, E. Beltrami, in �Mathematics for Dynamic Modeling� (2^nd edition) Academic Press, Boston, Ch 7, pp 153-183, 1998.
Proceedings of the Third International Pamir Conference on Transfer Phenomena in Magnetohydrodynamic and Electroconducting Flows, Sept. 22-26, 1997, Aussois, France, Vol.1-2, Sections 3-7, pp 45-196, LEGI, Grenoble, France 1997.
Applications of Magnetoelectrolysis, R. A. Tacken and L. J. J. Janssen, "Journal of Applied Electrochemistry" Vol. 25, pp 1-5, 1995.
Magnetoelectrolysis, T. Z. Fahidy, "Journal of Applied Electrochemistry" Vol. 13, pp 553-563, 1983.
In April 2008, about 170 entries were listed under the heading of �magnetoelectrolysis�, and 297,000 entries under the heading of �magnetic field effects on electrolysis� by the altavista.com search engine.

Listings of electrochemistry books, review chapters, proceedings volumes, and full text of some historical publications are also available in the Electrochemistry Science and Technology Information Resource (ESTIR). (http://knowledge.electrochem.org/estir/)

Return to: Top – Encyclopedia Home Page – Table of Contents – Author Index – Subject Index – Search – Dictionary – ESTIR Home Page – ECS Home Page