Historical introductionElectrochemical capacitors provide a mode of electrical charge- and energy-storage and delivery, complementary to that by batteries. The first electrochemical capacitor device was disclosed in a General Electric Co. patent in 1957 to Becker but was of a crude nature, employing porous carbon. Later work by Sohio (1969) described a so-called "electrokinetic capacitor" utilizing porous carbon in a non-aqueous electrolyte which enabled it to be charged up to about 3 V, though the operation of the device was not "electrokinetic" in nature, a misnomer. In 1971, Trasatti and Buzzanca recognized that the electrochemical charging behavior of ruthenium dioxide films was like that of capacitors. Between 1975 and 1980, the present author and his co-workers, under contract with the then Continental Group Inc., carried out extensive fundamental and development work on the ruthenium oxide type of electrochemical capacitor (Conway, 1997) which behaves as a surface- redox pseudocapacitance (see below). The whole field has burgeoned since about 1990 and is very active in fundamental, and R&D directions.A great deal of scientific and technological research has been reported in the scientific literature since about 1990. An extensive and detailed account of this has been given in the author's monograph on "Electrochemical Supercapacitors: Scientific Fundamentals and Technological Applications" (1999).
Scientific introductionIn order to describe "electrochemical capacitors" and to explain their function and applications, it is necessary first to consider the nature of an ordinary electrostatic capacitor or a "condenser" as it used to be called, and thence the meaning of the term electrical capacitance.The nature of electricity took a long time to be understood, from the early experiments on electrostatic electricity in the mid-18th century, for example by Galvani, through the time of the invention of the first electric battery by Alessandro Volta (Volta's "Pile") in 1800, on to Faradays's and Davy's monumental discoveries on the chemical origin of electricity generated by Volta's pile. At first, two "kinds" of electricity were postulated: "animal electricity", as in the works of Galvani on stimulation of the frog's leg nerve by contact between two dissimilar metals and later, "Voltaic electricity" generated chemically from a Volta pile of zinc and silver or copper plates separated by paper wetted with an acid or salt solution (Conway, 2000). In parallel with these discoveries were extensive works on electrostatic electricity generated for example by the rubbing of naturally occurring amber or by the so-called Wimshurst machine (a rotating circular plate, containing insets of amber-like material, rubbing against charge-collector plates connected overall to a Leyden Jar or a spark-gap). It was from this direction of research on electricity that the invention of the electric condenser arose, referred to as the "Leyden Jar", and capable of storing electric charge generated by a Wimshurst machine. Such a jar had the "capacity", depending on its dimensions and materials of construction, of storing electric charge by bringing it together in a condensed way (hence the term "condenser") on the surfaces of a Leyden Jar at a certain two-dimensional charge density. The principle of design and operation of the Leyden Jar and all subsequent regular condensers or capacitor devices, is as follows. Two metal surfaces that constitute electrodes are separated at some small distance either in air (or vacuum) or on each side of a liquid or solid film, referred to as the "dielectric", a term first used by Michael Faraday . For a given separation of the electrode plates, the capacitance developed per unit area of the two plates depends on the properties of the dielectric between the plates characterized by its so-called dielectric constant.
The nature of electric charge remained elusive until much later (1897) when J.J. Thomson identified and characterized the fundamental entity of electric charge as the "electron", present ubiquitously in all atoms of the Universe and identified, in his experiments, by means of experiments on gases at low pressures in gas-discharge tubes (Crookes tubes or neon lights). The electron charge was determined independently by Townsend and by Millikan (Glasstone, 1940), and was shown to be equivalent to Faraday's constant for the relation between extent of passage of charge and extent of chemical change (as related by Faraday's Laws) caused by electrolysis of conducting solutions, when calculated on a "per gram-atom" or "gram-equivalent" basis.
Relation of capacitance to geometry and dielectric constant of a capacitorThe capacitance of a capacitor is proportional to the area of the contact plates and the dielectric constant of the medium between the plates, and it is inversely proportional to the separation between the plates (see the Appendix). In relation to electrochemical capacitors, to be discussed below, the capacitance of small dielectric capacitors is very small being on the order of microfarads or nanofarads (millionth or billionth of a farad, respectively) for small devices on the order of mm or cm in dimensions. By having very thin insulating films, on the order of 10 to 100 nanometers, formed anodically on the plate of a two-electrode capacitor, substantially larger specific capacitances (that is per /cm2) can be attained. Such devices are called "electrolytic capacitors" because the thin dielectric oxide films are formed on the plates by an anodic electrolysis procedure applied at metals such as aluminum, tantalum, titanium, niobium, etc. Such capacitors are still of the dielectric type (the dielectric medium being here the thin, insulating oxide film, usually having a relatively high dielectric constant) and should not be confused with the "electrochemical" capacitor type of device which is the topic of this article.Electrochemical capacitors are a special kind of capacitor based on charging and discharging the interfaces of high specific-area materials such as porous carbon materials or porous oxides of some metals. They can store electric charge and corresponding energy at high densities in an highly reversible way, as does a regular capacitor, and hence can be operated at specific power densities (in watts/kg) substantially higher than can most batteries. Their capacitance for a given size of the device is thus much higher, by a factor of 10,000 or so, than those achievable with regular capacitors. For this reason proprietary names such as "Supercapacitors" or "Ultracapacitors" have been coined to describe their performance. While they function formally like rechargeable batteries in storing or delivering electric charge, their mechanisms of charge storage are quite different, in most cases, from those operating in batteries. Thus, electrochemical capacitors are not substitutes for batteries but rather are to be regarded as complementary to them for charge storage or delivery. They can offer advantageously fast charging or discharging rates over most batteries of comparable volume but their energy density is usually less, by a factor of 3 to 4, than that of batteries. Their high power or power densities, however, enables them to be employed in interesting complementary ways in hybrid systems with batteries. An important difference between charging a capacitor and charging a battery is that there is always an intrinsic increase of voltage on charge (or decrease on discharge) of a capacitor as the charge per cm2 is increased or decreased. In contrast, an ideal battery has a constant voltage during discharge or recharge except as the state of charge approaches 0 or 100%. Although practical batteries exhibit some dependence of cell voltage on state of charge, especially lithium-intercalation batteries, the latter for fundamental reasons arising from intercalation. (See the Appendix for further details.)
The double-layer capacitance at electrode interfaces
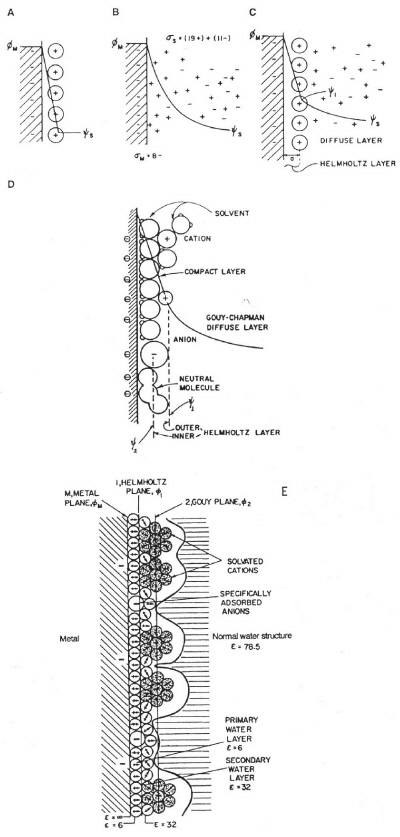
double-layer capacitance that arises at all electrode interfaces with electrolyte solutions or ionic melts. The concept and model of the double layer arose in the work of von Helmholtz (1853) on the interfaces of colloidal suspensions and was subsequently extended to surfaces of metal electrodes by Gouy, Chapman, and Stern, and later in the notable work of Grahame around 1947. Models of the double layer are shown in Figure 2, with their capacitor-like structures.
|
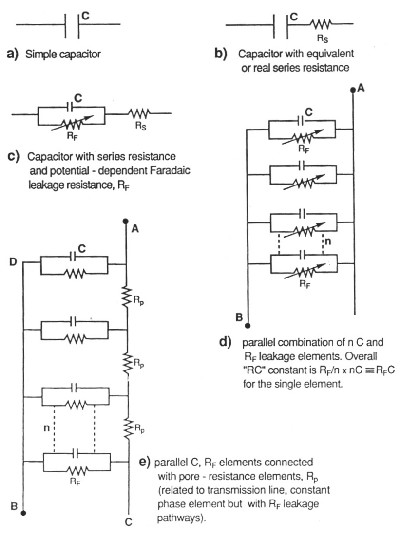 |
| Fig. 3. Hierarchy of equivalent circuits for capacitors and electrochemical capacitors showing "transmission-line" circuit for the latter, in the case of a porous carbon electrode. |
The presence of real or equivalent series resistance in the operating equivalent circuit of any capacitor introduces an ir potential drop in the process of charging or discharging and this drop depends, of course, on the charging rate (current) leading to distortion of the charging curve of accumulated charge against voltage, in time. When the distributed resistance effect also operates, as it normally does, the distortion effect becomes more complex but has been experimentally and computationally evaluated (de Levie, 1963).
The above effect causes limitation of rates at which the capacitor can be charged or discharged and, for ac modulated charging, it also introduces a frequency-dependent phase angle (normally -90o) between the modulated applied voltage and the resultant charging current. This also applies to other, non-constant charging modes.
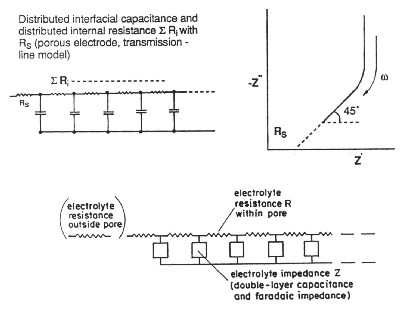 |
| Fig. 4. de Levie transmission-line model for resistance/capacitance matrix in an high-area porous electrode. |
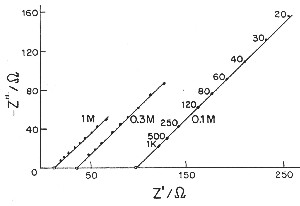 |
| Fig. 5. Complex-plane impedance plots (imaginary capacitive component against real ohmic component) for a porous electrode according to de Levie. |
de Levie has pointed out that the distributed R/C effect in porous electrodes is equivalent to restrictions of power due to ohmic ir drop (that is the potential drop due to current passing through resistive elements in the matrix). Thus there is a "penetration effect" into the electrode matrix due to attenuation of for example a modulation or time-dependent transient charging voltage so that not all of the depth or width, or diameter of the electrode structure is subject to a uniform charging rate. This introduces a non-chemical irreversibility in the charge/discharge behavior of the electrochemical capacitor device which is electrically demonstrable.
It must be stated, however, that in state-of-the-art developments of electrochemical capacitors, using aqueous-solution electrolytes, the above distributed-resistance effect has been substantially minimized so that devices having high operating power have been successfully engineered and marketed. Nevertheless, with non-aqueous electrolyte capacitors, which have higher operating voltages up to 3.0 to 3.5 V (hence 9 to 12 times energy density which depends on the square of maximum operating voltage), the distributed ohmic effects are more significant so that achievable operating power levels are less than those attainable with aqueous electrolyte devices.
Electrochemical capacitors based on pseudocapacitance
A different kind of capacitance can arise at electrodes of certain kinds, for example ruthenium dioxide, when the extent of faradaically admitted charge depends linearly, or approximately linearly, on the applied voltage. For such a situation, the electrode behavior is equivalent to, and measurable as, a capacitance. This capacitance can be large but it is faradaic and not electrostatic (that is non-faradaic) in origin. This is hence an important difference from the nature of double-layer capacitance, so it is called "pseudocapacitance". This kind of pseudocapacitance can originate when an electrochemical charge-transfer process takes place to an extent limited by a finite quantity of reagent or of available surface. Several examples of pseudocapacitance can arise, but the capacitance function is usually not constant and, in fact, is usually appreciably dependent on potential or state of charge.
However, when the process is surface limited, and is proceeding in several one-electron stages, a broad range of significant capacitance values arises as is found with ruthenium dioxide electrodes where the pseudocapacitance is almost constant (within 5%) over the full operating voltage range. Some other metal oxides behave similarly but only over smaller operating voltage ranges. The ruthenium dioxide pseudocapacitance provides one of the best examples of electrochemical (pseudo)capacitance as, in addition to the almost constant capacitance over a wide voltage range, its reversibility is excellent, with a cycle life over several hundred-thousand cycles. Furthermore, the pseudocapacitance can increase the capacitance of an electrochemical capacitor by as much as an order of magnitude over that of the double-layer capacitance. However, its cost prevents its large-scale use so that it has been employed mainly in military applications.
Another type of material exhibiting pseudocapacitive behavior that is highly reversible is the family of conducting polymers such as polyaniline or derivatives of polythiophene. These are cheaper than ruthenium dioxide but are less stable, giving only thousands of cycles (still quite attractive) over a wide voltage range. (See the Appendix for a more detailed discussion of the pseudocapacitance.)
Applications and technology
 Fabrication of electrochemical capacitors
Fabrication of electrochemical capacitors
General industrial production of electrochemical capacitors follows that of battery cell procedures with automatic production-line machinery. Cell designs are of various kinds including cylindrical, prismatic, button, or coin types, with some larger embodiments being of cake-tin sizes or larger, and some multi-cell series for higher voltage with bipolar electrodes having edge seals. In series configurations for high-voltage applications, balancing of unit cell performance and behavior is a technological challenge.
 Hybrid systems
Hybrid systems
The high power-density capability of electrochemical capacitors has led them to be employed in hybrid configurations with batteries and fuel cells in a load-leveling function, for example in electric vehicles. The capacitor component, suitably coupled with a battery or fuel cell, provides the necessary power density for up-hill or accelerative driving while regenerative braking provides a certain extent of recharging.
Another type of hybrid system is where ruthenium dioxide is used as a second oxide component, acting as a pseudocapacitance in electrolytic capacitors (the Evans Hybrid Capacitor). This gives indirectly, an improved capacitance density for the overall two-electrode device.
Another interesting hybrid type, currently under investigation in our own and other laboratories, is a combination of a double-layer carbon (electrochemical capacitor) electrode combined to work against a rechargeable battery electrode, for example a lead-acid positive plate (acidic solution) or a nickel battery positive plate (alkaline solution). This type of device (called an asymmetric capacitor) enables almost all of the charge residing on the capacitor-type electrode to be utilized on discharge in contrast to the battery-type electrode while, with a symmetrical capacitor made with two similar double-layer capacitance electrodes, each electrode is only half discharged from its initial voltage, relative to the other electrode, when the cell discharge voltage reaches zero, therefore delivering less electrical energy than the hybrid.
Another application is in electrical research experiments where very high energy and high-rate discharges are required, for example through gases for high-energy spark or arc generation.
A variety of other applications has been envisaged in the literature (Conway, 1999). Examples are: cold-start assist for diesel locomotives; emergency back-up power for computer systems; stationary power-system load leveling or bridging for short-period power outages; energy source for initial heating of catalytic converter units; energy collection and storage from windmill dynamos.
For society at large, the use of capacitor/battery hybrid systems for improvement of electric-vehicle (EV) performance will assist the adoption of EV transportation systems with zero or diminished nitrogen oxide and carbon dioxide atmospheric contamination. However, such a transition to an "EV lifestyle" will probably not become substantial for another one to two decades.
 Relation of capacitance to geometry and dielectric constant of a capacitor
Relation of capacitance to geometry and dielectric constant of a capacitor
The capacitance "C" of a capacitor depends on a) the area "A" of the contact plates, b) the separation "d" between the plates (when parallel), and c) the dielectric constant "ε" of the medium between the plates (limitingly vacuum, for which "ε" is taken as 1; for all other materials, including gases, ε > 1). The relationship between "C" and the above quantities is given by the simple equation (Conway 1999)
[1] ![]() C = A ε / 4 π d
C = A ε / 4 π d
or, in terms of so-called rationalized units,
[2] ![]() C = Aε εo / d
C = Aε εo / d
where εo (= 8.84 × 10-12 farads/m) is the dielectric permittivity of free space. The units of "C" are in farads or coulombs per volt, that is coulombs stored by the capacitor per volt across its two electrodes.
An important difference between charging a capacitor and charging a battery is that there is always an intrinsic increase of voltage "V" on charge (or decrease on discharge) of a capacitor as the charge per cm2 is increased or decreased, according to Equation [3] which defines the relation between capacitance "C" and the inter-plate voltage "V" that arises from accumulation of a charge "q":
![]() Some important differences between capacitors and batteries
Some important differences between capacitors and batteries
[3] ![]() C = q/V or q = CV
C = q/V or q = CV
In contrast, an ideal battery has a constant voltage during discharge or recharge except as the state of charge approaches 0 or 100%. (Practically, most batteries exhibit some dependence of cell voltage on state of charge, especially lithium-intercalation batteries, the latter for fundamental reasons arising from intercalation).
The consequence of the above difference, based on Equation [3], is that the energy stored by a capacitor is 1/2 CV2 or 1/2 qV while, for a battery, the corresponding stored energy (or energy density) is qΔV, twice as much as that for a capacitor charged to the same cell voltage "ΔV". Thus, the stored energy in a capacitor device increases as the square of the cell voltage "V" as charge is accumulated. This is an important difference between capacitor and battery cell behavior and affects the interfacing between such systems in hybrid devices.
It was noted above that the energy stored in a capacitor cell, charged to a voltage "V" is 1/2 CV2 and "V" increases as charge "q" accumulates on its plates determined by "C". The charging energy 1/2 CV2 arises in the following way. For a capacitor being charged from an initial voltage V = 0 to a final value "Vf" the energy "E" stored will be a free-energy "G" (charge times voltage):
[4] ![]()
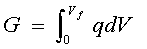
At any state of charge, q = CV (Equation [3]), so that
[5] ![]()
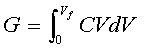
[6] ![]() G = 1/2CVf2
G = 1/2CVf2
The charge density "q" (coulomb/cm2) of electrons and ions at the interface is dependent on the potential difference, ΔΦ, across this double layer so that a differential capacitance "Cdl" arises determined by
![]() Double-layer capacitance
Double-layer capacitance
[7] ![]() Cdl = dq/d(ΔΦ) or Δq/ΔΦ
Cdl = dq/d(ΔΦ) or Δq/ΔΦ
The difference of potential extends beyond the immediate layer of solvated ions in the compact, capacitor-like (Helmholtz) region, out into solution, so that a further diffuse-layer capacitance "Cdiff" arises. It combines with the capacitance of Helmholtz region "CH" in series, electrically, so that
[8] ![]()
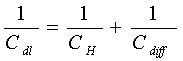
A different kind of capacitance can arise at electrodes of certain kinds, for example ruthenium dioxide, when the extent of faradaically admitted charge "q" depends linearly, or approximately linearly, on the applied voltage "V". For such a situation, there is a mathematical derivative, dq/dV that would be constant, which is equivalent to, and measurable as, a capacitance (see Equation [3]). This capacitance, denoted by "CΦ", can be large but it is faradaic and not electrostatic (that is non-faradaic) in origin. This is hence an important difference from the nature of double-layer capacitance "C" or "Cdl" so it is called "pseudocapacitance". The pseudocapacitance can increase the capacitance of an electrochemical capacitor by as much as an order of magnitude over that of the double-layer capacitance.
![]() Pseudocapacitance
Pseudocapacitance
This kind of pseudocapacitance can originate when an electrochemical charge-transfer process takes place to an extent limited by a finite quantity of reagent or of available surface, the latter in the case of adsorption (for example of hydrogen), with charge transfer. Several examples of pseudocapacitance can arise as follows, but the "CΦ" function is usually not constant and, in fact, is usually appreciably dependent on potential or state of charge.
a) When an electrochemical adsorption process, arising from charge transfer, takes place at an electrode surface, for example in the process of electrosorption of H atoms discharged at Pt electrode surfaces in aqueous acid solution by the process:
[9] ![]() H3O+ + Pt + e- ==> H2O + Pt/H
H3O+ + Pt + e- ==> H2O + Pt/H
so-called underpotential deposition since the above reaction takes place over a potential range "ΔV" of about 0.35 V positive to the equilibrium potential for H2 gas evolution in the electrolysis of water.
Fractional H coverages "Θ" at Pt can increase continuously, over the above electrode potential range, from 0 to 1, prior to evolution of H2 and each atom of H deposited requires passage of one electron of electric charge. Hence, a pseudocapacitance "CΦ" arises from the relation between charge passed "q" and "ΔV", and "q" is faradaically related to the coverage fraction "Θ" of electrodeposited H. A full monolayer (Θ ==> 1) of H requires passage of about 210 µC of charge "q1" per cm2 of a smooth Pt surface.
[10] ![]() CΦ = q1 dΘ/dΔV
CΦ = q1 dΘ/dΔV
"Θ" is related to electrode potential "V" by the relation
[11] ![]() Θ/(1 - Θ) = K exp (VF/RT)
Θ/(1 - Θ) = K exp (VF/RT)
b) A number of electrochemical reactions involving species in solution, such as Fe+++/Fe++ or [Fe(CN)6]3-/[Fe(CN)6]4-, known as redox processes, take place at inert electrodes, for example Au or Pt, with a logarithmic relation (the Nernst equation) between the extents of oxidation/reduction between the redox couple pair of ions. Thus, for example
[12] ![]() E = Eo + (RT/F) ln a[Fe(CN)6]3-/a[Fe(CN)6]4-
E = Eo + (RT/F) ln a[Fe(CN)6]3-/a[Fe(CN)6]4-
where "a" represents the respective activities of the two ions of the redox couple. The above Equation [11] can be rearranged in terms of the fractions of a given chemical quantity of the redox ions in the reversible reaction
[13] ![]() [Fe(CN)6]3- + e- <==> [Fe(CN)6]4-
[Fe(CN)6]3- + e- <==> [Fe(CN)6]4-
that exist in the course of reduction (or reoxidation) as a function of the potential "E" in relation to its so-called standard value "Eo" in Equation [12]. E = Eo when the reagent ion activities (concentrations) are equal so that the ln function is zero. The rearranged form of Equation [11] is in terms of the molar quantities "Qox" and "Qred" in relation to the total reagents Qox + Qred (= Q) and reads
[14] ![]()
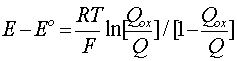
with Qred/Q = 1 - Qox/Q. Then it is seen that Equation [14] has the same form as that of Equation [11] (after taking logarithms) for electrosorption and its derivative is a capacitance quantity.
c) A similar logarithmic relation in X / (1 - X) applies to absorption of Li+ ions into Li-intercalation hosts in Li-ion battery electrochemistry where "X" is the fractional occupancy of available intercalation sites in the intercalation host material, for example TiS2, CoO2, etc. Hence, Li+ ion intercalation formally exhibits a pseudocapacitance, though the Li+ ion systems are normally referred to as battery devices.
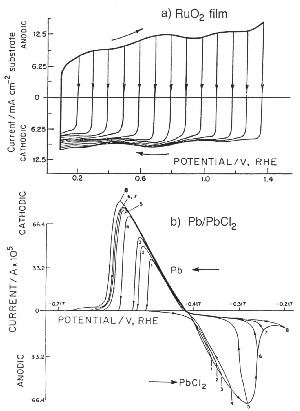 |
| Fig. 6. Comparison of cyclic voltammetry behavior of a reversibly chargeable electrochemical capacitor material (RuO2) and a battery-type (Pb/PbCl2) like in the lead-acid battery. |
However, when the redox process is a surface one, proceeding in several one electron stages, a much broader range (1.4 V) of significant "CΦ" values arises as is found with RuO2 electrodes where "CΦ" is almost constant within 5% over that voltage range. Some other transition-metal oxides behave similarly but only over smaller operating voltage ranges, about 0.6 to 0.8 V (Conway, 1997).
The case of RuO2 pseudocapacitance provides one of the best examples of electrochemical (pseudo)capacitance as its "CΦ" is almost constant over a 1.4 V voltage (Figure 6) range and its reversibility is excellent, with a cycle life over several hundred-thousand cycles. However, its cost prevents its large-scale use so that it has been employed mainly in military applications.
Another type of material exhibiting quasi-redox behavior that is highly reversible is the family of conducting polymers such as polyaniline or derivatives of polythiophene. These are cheaper than ruthenium dioxide but are less stable, giving only thousands of cycles (still quite attractive) over a voltage range between 0.8 V and up to 3.0 V for some materials.
Figure 6 shows the contrast between a reversibly charged electrochemical capacitor material (RuO2) and an irreversibly chargeable battery-type material (Pb/PbCl2).
Related article
Electrolytic capacitorsBibliography
- Power Limitations of Supercapacitor Operation Associated with Resistance and Capacitance Distribution in porous Electrode Devices, W. G. Pell and B. E. Conway, "Journal of Power Sources" Vol. 105, pp 169-181, 2002.
- Advances in Electrochemical Capacitors and Hybrid Power Systems, R. J. Brodd, D. H. Doughty, K. Naoi, M. Morita, C. Nanjundiah, J. H. Kim, and G. Nagasubramanian (editors), The Electrochemical Society Proceedings, Vol. 2002-7, Pennington, NJ, 2002.
- Bicentennial of Alessandro Volta's Invention of the "Electric Pile", B. E. Conway, "Canadian Chemical News" Vol. 52, No. 1, pp 15-17, January 2000.
Available at: http://www.accn.ca/accn2000/january2000/pg12-22.pdf (the second article in the file). - Electrochemical Supercapacitors: Scientific Fundamentals and Technological Applications, B. E. Conway, Kluwer Academic/Plenum Publishing, New York, 1999.
- The Role and Utilization of Pseudocapacitance for Energy Storage by Supercapacitors, B. E. Conway, V. Birss, and J. Wojtowicz, "Journal of Power Sources" Vol. 66, pp 1-14, 1997.
- Ruthenium Dioxide: a New Interesting Electrode Material, Solid State Structure and Electrochemical Behavior, S. Trasatti and G. Buzzanca, "Journal of Electroanalytical Chemistry" Vol. 29, pp A1-A5, 1971.
- Michael Faraday, a Biography, L. Pearce Williams, Chapman and Hall, London, 1965.
- On Porous Electrodes in Electrolyte Solutions, R. de Levie, "Electrochimica Acta" Vol. 8, pp 751-780, 1963.
- Low Voltage Electrolytic Capacitor, H. L. Becker, U.S. Patent 2,800,616, 1957.
- Equilibrium Properties of Electrified Interfaces, R. Parsons, in "Modern Aspects of Electrochemistry" Vol. 1, pp 103-179, J. O'M. Bockris (editor), Butterworths, London, 1954.
- The Electrical Double Layer and the Theory of Electrocapillarity, D. C. Grahame, "Chemical Reviews" Vol. 41, pp 441-501, 1947. Available on the WWW.
- Physical Chemistry, (Chapter 1) S. Glasstone, MacMillan, London, 1940.
- Leyden Jar, "Encyclopaedia Britannica" Vol. 13, p 989, 1929.
- Zur Theorie der Elektrolytischen Doppelschicht, O. Stern, �Zeitschrift f�r Elektrochemie and angewandte physikalische Chemie� Vol. 30, pp 508-516, 1924. Available on the WWW.
- The Electron in Chemistry, J. J. Thomson, Chapman and Hall, London, 1923.
- A Contribution to the Theory of Electrocapillarity, D. L. Chapman, �The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science� Ser. 6, Vol. 25, pp 475-481, 1913. Available on the WWW.
- Sur la constitution de la charge �lectrique � la surface d'un �lectrolyte, L. G. Gouy, �Journal de Physique Th�orique et Appliqu�e� Ser. 4, Vol. 9, pp 457-468, 1910. Available on the WWW.
- Sur la constitution de la charge �lectrique � la surface d'un �lectrolyte, L. G. Gouy, �Comptes rendus hebdomadaires des s�ances de l'Acad�mie des sciences, Paris� Vol. 149, pp 654-657, 1909. Available on the WWW.
- On the Charge of Electricity Carried by Gaseous Ions, J. J. Thomson, "Philosophical Magazine" Vol. 5, pp 346-355, 1903.
- Ueber einige Gesetze der Vertheilung elektrischer Str�me in k�rperlichen Leitern mit Anwendung auf die thierisch-elektrischen Versuche (in German), H. von Helmholtz, "Annalen der Physik und Chemie, Leipzig" Vol. 89, pp 211-233, 1853. Available on the WWW.
Listings of electrochemistry books, review chapters, proceedings volumes, and full text of some historical publications are also available in the Electrochemistry Science and Technology Information Resource (ESTIR). (http://knowledge.electrochem.org/estir/)
Return to: Top – Encyclopedia Home Page – Table of Contents – Author Index – Subject Index – Search – Dictionary – ESTIR Home Page – ECS Home Page
ECS | Redcat Blog | ECS Digital Library